「人工智能导论」期末复习
本文最后更新于:2023年4月15日 晚上
0 | 考纲
1 | 绪论
1.0 | 考题
- 人工智能定义
- 举出5个人工智能方面的应用并简单介绍
- 简述人工智能三大学派及其观点
1.1 | 人工智能三大学派
图灵的学术贡献:
- 1936发表论文, 提出图灵机理论
- 1950年发表论文, 提出图灵测试
1956年达特矛斯会议「人工智能」正式诞生
符号学派, 连接学派, 行为学派
符号学派认为人工智能源于数理逻辑, 代表人物: 纽厄尔, 肖, 西蒙, 尼尔逊
连接学派认为人工智能源于仿生学(神经网络), 代表人物: 麦克洛奇, 皮兹
行为学派认为人工智能只是在与环境的交互作用中表现出来, 代表人物: 布鲁克(Brooks)研制的机器虫
2 | 知识表示
2.0 | 考题
- 至少简述四种知识表示方法及其特点
- 什么是本原问题
2.1 | 知识表示方法
知识表示方法: 状态空间法, 问题归约法, 谓词逻辑法, 语义网络法
知识: 把有关信息关联在一起所形成的信息结构
知识表示: 计算机可以接受的用于描述知识的数据结构
状态空间法三要素: 状态, 算符, 状态空间方法
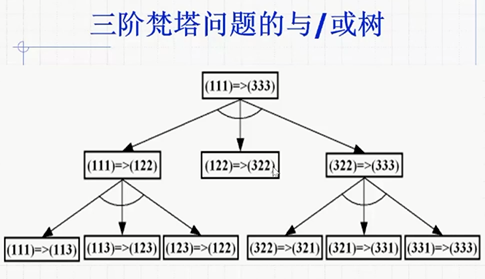
问题归约法: 从要解决的问题出发, 把问题归成一个个直接可解的本原问题(本原问题: 不能再分解或变换且直接可解的子问题), 代表: 汉诺塔/梵塔问题
语义网络: 是知识的一种图解表示, 它由节点和弧线组成, 节点用于表示实体, 概念和情况等, 弧线用于表示节点间的关系
3 | 经典逻辑推理
3.0 | 考题
2道必考题:
归结反演的大题
用谓词逻辑表示下列句子
3.1 | 代换(置换)
代换是一个形如
的有限集合
其中$t_i$是项(常量, 变量, 函数)
$x_i$为某一公式中互不相同的变元
3.2 | 合一
设有公式集
若存在一个代换$\lambda$使$F_1\lambda=F_2\lambda=\cdots=F_n\lambda$
则称$\lambda$为公式集F的一个合一, 且称$F_1, F_2, \cdots, F_n$是可合一的
3.3 | 自然演绎推理
自然演绎推理的最基本的推理规则是三段论推理, 包括:
- 假言推理
- 拒取式
- 假言三段论
假言推理: $P, P \rightarrow Q \Rightarrow Q$
拒取式: $P \rightarrow Q, \lnot Q \Rightarrow \lnot P$
假言三断论: $P \rightarrow Q, Q \rightarrow R \Rightarrow P \rightarrow R$
3.4 | 归结演绎推理
需要证明$P \rightarrow Q$即$\lnot P \lor Q$的永真性, 根据反证法, 只需要证明其否定$P \land \lnot Q$的不满足性即可
子句的定义:
任何文字的析取式称为子句($A \lor B$)
子句集:
将谓词公式化为子句集的步骤
消去$\rightarrow$
将$\lnot$移动到紧靠谓词的位置上
- 重命名变元使得不同约束变元名字不同
- 消去$\exists$
- 若$\exists$不在$\forall$的辖域内, 用常量替换变元即$a/x$
- 若$\exists{y}$在$\forall{x}$的辖域内, 用skolem函数$f(x_1, x_2, \dots)$替换变元即$f(x)/y$
- 消去$\forall$化为合取范式
- 消去$\land$得到子句集
e.g.



利用归结反演的证明步骤
设F为已知前提的公式集,Q为目标公式(结论),用归结反演证明Q为真的步骤是:
否定Q,得到¬Q;
把¬Q并入到公式集F中,得到{F, ¬Q};
把公式集{F, ¬Q}化为子句集S;
应用归结原理对子句集S中的子句进行归结,并把每次归结得到的归结式都并入S中。如此反复进行,若出现了空子句,则停止归结,此时就证明了Q为真。
利用归结原理求取问题的答案
把已知前提用谓词公式表示出来,并且化为相应的子句集。设该子句集的名字为S。
把待求解的问题也用谓词公式表示出来,然后把它否定并与谓词Answer构成析取式。Answer是一个为了求解问题而专设的谓词。
把此析取式化为子句集,并且把该子句集并入到子句集S中,得到子句集S’。
对S’应用归结原理进行归结。
若得到归结式Answer,则答案就在Answer中。
e.g.
例:设A,B,C三人中有人从不说真话,也有人从不说假话。某人向这三人分别提出同一个问题:谁是说谎者?A答:“B和C都是说谎者”;B答:“A和C都是说谎者”;C答:“A和B中至少有一个是说谎者”。求谁是老实人,谁是说谎者?



4 | 不确定推理
4.0 | 考题
- 给你几个CF让你求一个CF, 需要用到的公式:
- 组合证据不确定度算法(and取小, or取大)
- 不确定性的传递算法
- 结论不确定性的合成算法
4.1 | 概率论基础公式
先验概率和后验概率:
先验概率: $P(A)$
后验概率: $P(A|B)$
条件概率:
全概率公式:
对任何事件B有下式成立:
贝叶斯公式:
若事件$A_i$满足全概率公式的条件, 则对任何事件B有下式成立
4.2 | 主观贝叶斯方法
这里老师说不考, 哭了, 白看一天
形式:
其中$E$表示规则前提条件, $H$是结论
$LS$是规则的充分性度量, 定义为:
$LS$指出了$E$对$H$的支持程度
LN是规则的必要性度量, 定义为:
$LN$指出了$\lnot E$对$H$的支持程度
几率函数:
几率函数$O(X)$
引入几率函数后得到:
可以推出如下公式:
例题
这部分公式太多太复杂了, 往年也没见考, 把例题里面的公式背背感觉就差不多了…

首先先推出推理网络如下:
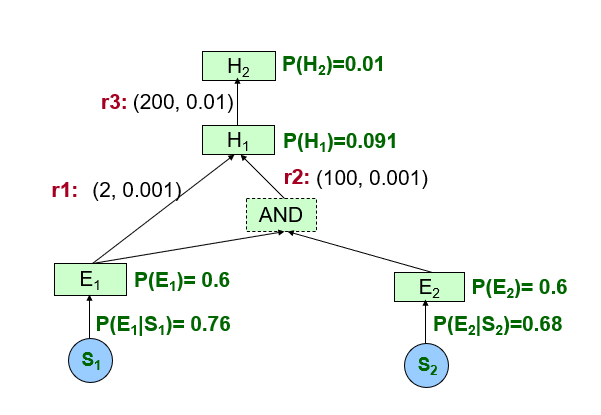
可知我们计算最后的P(H2 | S1, S2), 需要提前知道:
- $P(H_1|S_1)$
- $P(H_1|(S_1 \text{AND} S_2))$
- $P(H_1|S_1,S_2)$
- $P(H_2|S_1,S2)$
计算P(H1|S1)
依据得公式:
EH公式即 (考试会给)
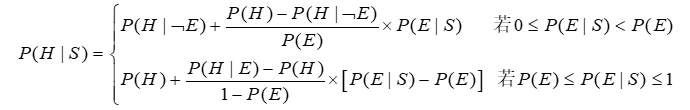
$P(H|E)=\frac{LS \times P(H)}{(LS-1) \times P(H)+1}$
故得到答案:
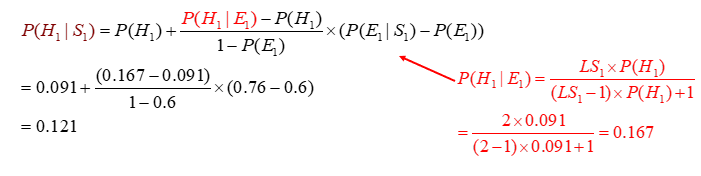
计算P(H1|S1 AND S2)
这里涉及到合取的证据, 方法是比较P(E1|S1)和P(E2|S2), 取最小的考虑就行, 这里P(E1|S1) = 0.76< P(E2|S2) = 0.68, 故只考虑E2对H1得影响, 即P(H1|S1 AND S2) = P(H1 | S2)
接下来算法和第一个相同

计算P(H1 | S1, S2)
这里涉及到一个新公式…叫「结论不确定性的合成」
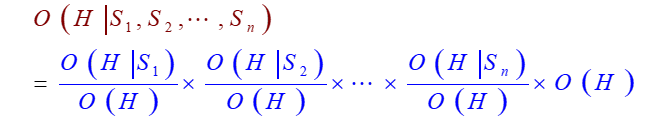
故这里计算P(H1 | S1, S2), 首先得计算O(H1 | S1, S2)

然后再根据$P(X) = \frac{O(X)}{1+O(X)}$
得到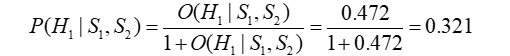
计算P(H2|S1,S2)
知道了H2的前件为H1后, 我们可以直接用EH公式搞定…

太复杂了, 计算量也很大, 千万别考啊啊啊
4.3 | 可信度方法
形式:
$CF(H,E)$指该知识的可信度, 称为可信度因子/静态强度, 范围在-1~1
$CF(H,E)$定义为:
其中MB为信任增长度, MD为不信任增长度
组合证据不确定度算法

不确定性的传递算法
在$IF\,\,E\,\,THEN\,\,H\,\, (CF(H,E))$中
结论$H$的可信度由下式计算
结论不确定性的合成算法
懒得码字了, 直接上ppt..

典型例题:
e.g.

解题步骤:
1 | |
4.4 | 带阈值和权值的可信度方法
形式:
解题方法:
和上面不同的地方在于:
- 带权值的知识计算组合不确定度的方法就是分别乘以权值然后加起来(注意这里w1 + w2 + … = 1)
- λ的作用就是CF(E)需要大于等于λ, 这条知识才能被运用, 如果小于λ, 就丢掉
直接上例题吧
e.g.

1 | |
5 | 模糊集
直接上题…
一般就是两种题型, 一种是模糊假言推理, 一种是模糊拒取式推理


方法就是给你俩模糊集A, B, 再给你一个A’或者B’, 让你构造一个R出来(公式会给), 然后如果是第一种情况x is A'就用B' = A' ° R得答案B', 如果是第二种情况y is B'就用A' = R ° B'得答案A'
两种构造R的方法:(扎德方法)
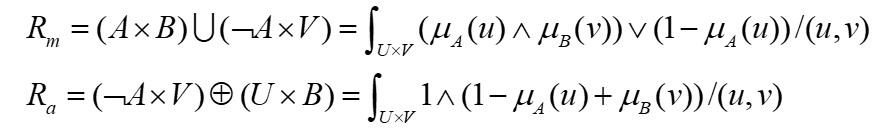
代码就是…
1 | |
关于A ° B这个公式, 叫做模糊关系得合成, 算法就是模拟矩阵乘法, 不过把相乘改成求小, 把相加改成求大
举个例子…

观察第一个元素, 实际上就是max{min(0.4, 0.2), min(0.5, 0.4), min(0.1, 0.6)} = 0.4
这部分得例题:
e.g.

1 | |
其中step2的Rm, Ra如下:

6 | 搜索
大概率考A*
三种搜索方式(DFA, BFS, A*), 让你画八数码问题的搜索树..
A*的h(x)有两种策略:
- 错放的棋子数
- 所有棋子与目标位置的曼哈顿距离之和
做题时候注意:
- 需要标出搜索状态的序号(从1开始)
- 需要标出原状态和目标状态
- A*的g(x)从0开始, 取值是搜索树当前层数-1, 即从初始状态到目前移动的步数
e.g.
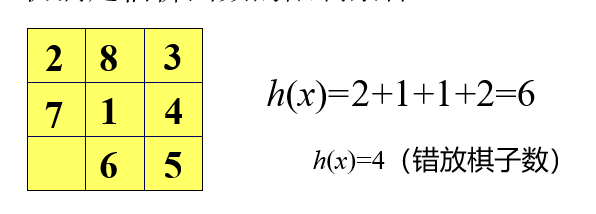
用A* + 错放棋子数得h(x), 对应的搜索树如下:
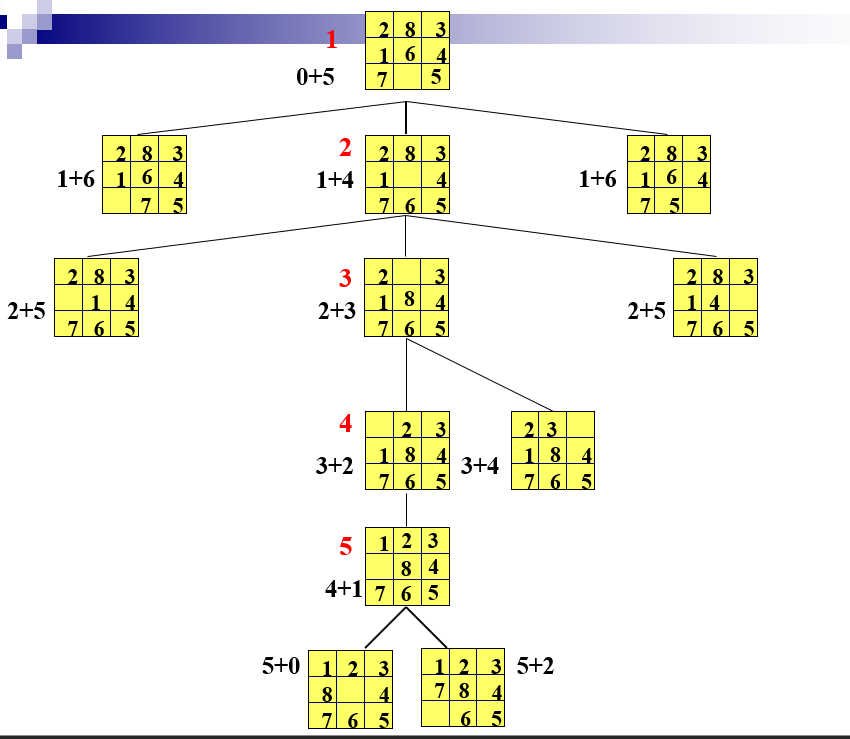
BFS得搜索树如下:
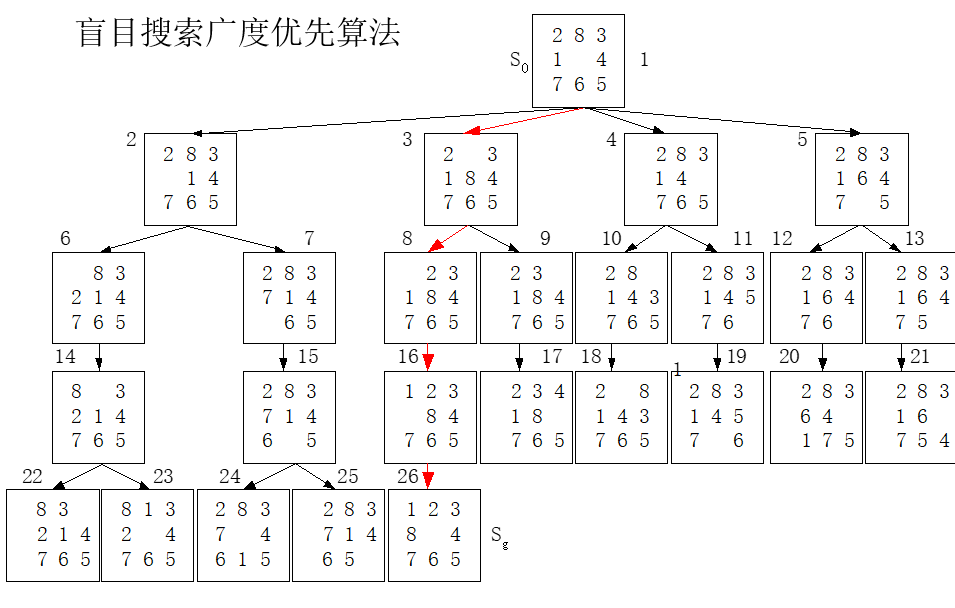
DFS得搜索树如下:(老师上课说画图不能提前猜到答案直接一路DFS直接搜到了, 所以我们要伪装一下…)
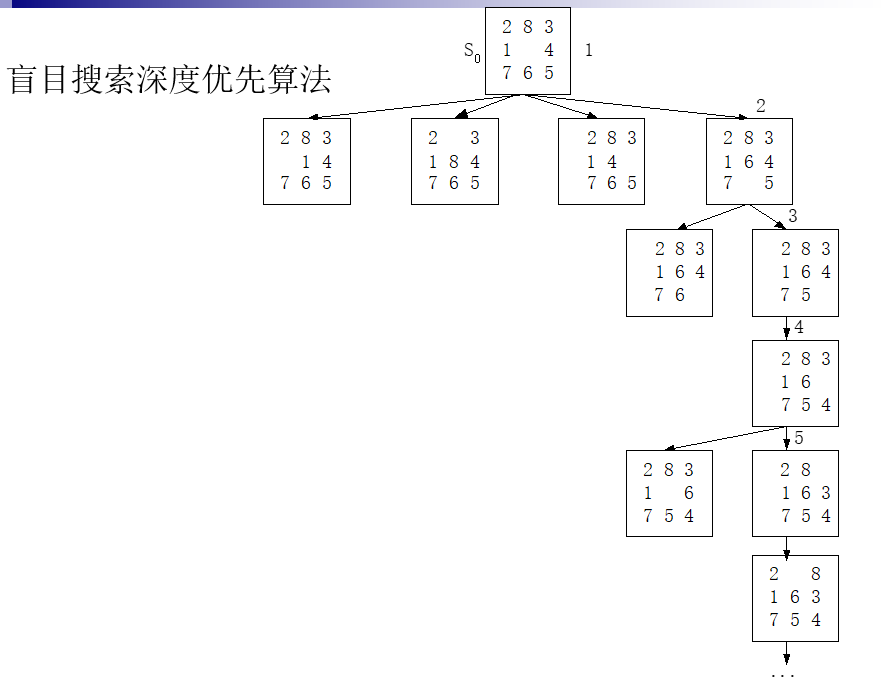
7 | 计算智能
根据老师的说法, 最后一道题应该是一个开放问题
谈谈计算智能的应用或者是什么之类的…算法可以用来干什么
alphago: 神经网络系统, 蒙特卡洛算法, 深度学习
分类, 数字识别, 图像识别
问题求解(下棋程序),逻辑推理与定理证明(四色定理证明),自然语言理解,自动程序设计,专家系统,机器学习,神经网络,机器人学(星际探索机器人),模式识别(手写识别,汽车牌照识别,指纹识别),机器视觉(机器装配,卫星图像处理),智能控制,智能检索,智能调度与指挥(汽车运输高度,列车编组指挥),系统与语言工具